Kaggle房价预测实践系列4-模型训练

现在进入到了正式的模型训练阶段，在面对一个问题时，选择什么样的模型来处理，也是很考量研究者的。截至目前为止，已经存在的各种各样正式发表的模型就有两千多个，每一种都一一尝试显然不现实。并且，拿不适用的模型处理不适用的数据，显然对我们要解决的问题来说南辕北辙。因此，我们往往在对问题的调研阶段就会确定问题的基本类型，同时调查在当前工业界和学术界解决这种类型问题主流的模型是什么、有哪些。此处，针对我们当前的问题，我们选择了7种模型，ridge 回归、svr 回归、gradient boosting 回归、random forest 回归、xgboost 回归、lightgbm 回归，它们都是当前应用在预测问题上比较出色的主流模型。

当然，除了对这7种模型的独立训练之外，我们还对它们进行了两种方式的融合，分别是 Stacking 和 Blending 融合。模型融合在一定程度是那个可以缓解独立模型的过拟合问题，提升模型的鲁棒性。

在正式开始模型训练前，我们首先设置交叉验证的折数，这里我们指定为12折：

kf = KFold(n_splits=12, random_state=42, shuffle=True)

其次，每个模型训练的过程都少不了评价指标的确定，本次我们选择 RMSE 均方根误差作为我们的评价指标。

def rmsle(y, y_pred):
    return np.sqrt(mean_squared_error(y, y_pred))

def cv_rmse(model, X=X):
    rmse = np.sqrt(-cross_val_score(model, X, train_labels, scoring="neg_mean_squared_error", cv=kf))
    return (rmse)

完成上面两步，我们就可以正式开始我们的训练了：

首先是决策树类型的模型定义：

# Light Gradient Boosting Regressor
lightgbm = LGBMRegressor(objective='regression', 
                       num_leaves=6,
                       learning_rate=0.01, 
                       n_estimators=7000,
                       max_bin=200, 
                       bagging_fraction=0.8,
                       bagging_freq=4, 
                       bagging_seed=8,
                       feature_fraction=0.2,
                       feature_fraction_seed=8,
                       min_sum_hessian_in_leaf = 11,
                       verbose=-1,
                       random_state=42)

# XGBoost Regressor
xgboost = XGBRegressor(learning_rate=0.01,
                       n_estimators=6000,
                       max_depth=4,
                       min_child_weight=0,
                       gamma=0.6,
                       subsample=0.7,
                       colsample_bytree=0.7,
                       objective='reg:linear',
                       nthread=-1,
                       scale_pos_weight=1,
                       seed=27,
                       reg_alpha=0.00006,
                       random_state=42)

# Gradient Boosting Regressor
gbr = GradientBoostingRegressor(n_estimators=6000,
                                learning_rate=0.01,
                                max_depth=4,
                                max_features='sqrt',
                                min_samples_leaf=15,
                                min_samples_split=10,
                                loss='huber',
                                random_state=42)  

# Random Forest Regressor
rf = RandomForestRegressor(n_estimators=1200,
                          max_depth=15,
                          min_samples_split=5,
                          min_samples_leaf=5,
                          max_features=None,
                          oob_score=True,
                          random_state=42)

接下来是线性回归类型的模型：

# Ridge Regressor
ridge_alphas = [1e-15, 1e-10, 1e-8, 9e-4, 7e-4, 5e-4, 3e-4, 1e-4, 1e-3, 5e-2, 1e-2, 0.1, 0.3, 1, 3, 5, 10, 15, 18, 20, 30, 50, 75, 100]
ridge = make_pipeline(RobustScaler(), RidgeCV(alphas=ridge_alphas, cv=kf))

以及支持向量机回归模型：

# Support Vector Regressor
svr = make_pipeline(RobustScaler(), SVR(C= 20, epsilon= 0.008, gamma=0.0003))

最后是 Stacking 融合模型：

# Stack up all the models above, optimized using xgboost
stack_gen = StackingCVRegressor(regressors=(xgboost, lightgbm, svr, ridge, gbr, rf),
                                meta_regressor=xgboost,
                                use_features_in_secondary=True)

有了定义好的模型，我们的工作就以及完成80%了，最辛苦的阶段过去大半，终于可以拿起咖啡，开启边喝咖啡边调参的悠闲生活了。依次执行模型训练过程，等待最终的打分结果。

scores = {}

score = cv_rmse(lightgbm)
print("lightgbm: {:.4f} ({:.4f})".format(score.mean(), score.std()))
scores['lgb'] = (score.mean(), score.std())

lightgbm: 0.1159 (0.0167)

score = cv_rmse(xgboost)
print("xgboost: {:.4f} ({:.4f})".format(score.mean(), score.std()))
scores['xgb'] = (score.mean(), score.std())

xgboost: 0.1364 (0.0175)

score = cv_rmse(svr)
print("SVR: {:.4f} ({:.4f})".format(score.mean(), score.std()))
scores['svr'] = (score.mean(), score.std())

SVR: 0.1095 (0.0198)

score = cv_rmse(ridge)
print("ridge: {:.4f} ({:.4f})".format(score.mean(), score.std()))
scores['ridge'] = (score.mean(), score.std())

ridge: 0.1101 (0.0161)

score = cv_rmse(rf)
print("rf: {:.4f} ({:.4f})".format(score.mean(), score.std()))
scores['rf'] = (score.mean(), score.std())

rf: 0.1366 (0.0188)

score = cv_rmse(gbr)
print("gbr: {:.4f} ({:.4f})".format(score.mean(), score.std()))
scores['gbr'] = (score.mean(), score.std())

gbr: 0.1121 (0.0164)

接下来是对训练数据进行模型拟合的阶段，有人会好奇，为什么前面的交叉验证以及对数据做了训练，并且也为模型打分了，为什么还需要对模型进行拟合呢？这样不是重复的进行拟合了吗？答案是为了对模型的参数调整得到最优组合，以应用到后面实际的拟合过程中。这好比问你，一个市场里有10家卖油桃的，哪一家最好吃？最可靠的方法就是我们到十家分别买一些，然后品尝，最后根据尝过之后的体验来给出结论以后到底要到哪一家再购买油桃。这个购买行为的开始，我们必须要指定一家作为开始购买的商家，通常我们会选择离市场入口最近的，那么，在我们的模型训练中就对应着设定模型参数初始值的过程，通常这个初始值往往是借鉴了很多前人的经验总结的公认最合适的参数组合。之后，就可以根据一些规则有选择的进行最优参数方向的调整了。这个过程对油桃挑选的方式选择，就对应了我们对训练数据十折交叉验证的过程，如果只拿最表面的，很明显在取样过程中有可能有局部偏差过大的情况，因为商家往往把漂亮、好的油桃放到表面招揽生意，而下面可能有很多较差的油桃，因此，为了更全面的评估油桃的情况，我们会从油桃堆里各处都拿一些，保证样本的均匀。同样的道理，我们的数据也需要均匀的抽取才对训练更可靠的模型参数有更大的帮助。

Stacking 模型略有不同，需要对前面的几个模型结果进行融合，并将融合的结果作为新的特征输入，才能训练得出自己的结果，所以，这里相当于需要连续执行7个模型，执行时间会比较久。

print('stack_gen')
stack_gen_model = stack_gen.fit(np.array(X), np.array(train_labels))

print('lightgbm')
lgb_model_full_data = lightgbm.fit(X, train_labels)

print('xgboost')
xgb_model_full_data = xgboost.fit(X, train_labels)

print('Svr')
svr_model_full_data = svr.fit(X, train_labels)

print('Ridge')
ridge_model_full_data = ridge.fit(X, train_labels)

print('RandomForest')
rf_model_full_data = rf.fit(X, train_labels)

print('GradientBoosting')
gbr_model_full_data = gbr.fit(X, train_labels)

进行完独立的模型拟合之后，为了保证模型的可靠性，让最终的预测结果具有更好的鲁棒性以避免过拟合，我们需要对模型进行混合。在对模型的混合阶段，大家往往对各个模型在混合时的权重有很多疑惑，依据什么确定呢？这个问题就见仁见智了，这里我们使用了交叉验证的得分作为参考，对表现好的模型增加权重，较差的模型减少权重。Stacking 因为关联到了所有模型的输出结果，因此我们认为它对预测的影响最大，权重最高。这个只是初步的解决方案，还可以在这个基础上根据 RMSE 的输出表现，做进一步的调整。

def blended_predictions(X):
    return ((0.1 * ridge_model_full_data.predict(X)) + \
            (0.2 * svr_model_full_data.predict(X)) + \
            (0.1 * gbr_model_full_data.predict(X)) + \
            (0.1 * xgb_model_full_data.predict(X)) + \
            (0.1 * lgb_model_full_data.predict(X)) + \
            (0.05 * rf_model_full_data.predict(X)) + \
            (0.35 * stack_gen_model.predict(np.array(X))))

打印混合模型得出的预测结果

blended_score = rmsle(train_labels, blended_predictions(X))
scores['blended'] = (blended_score, 0)
print('RMSLE score on train data:')
print(blended_score)

下面来看看各个模型最终表现的结果对比吧：

sns.set_style("white")
fig = plt.figure(figsize=(24, 12))

ax = sns.pointplot(x=list(scores.keys()), y=[score for score, _ in scores.values()], markers=['o'], linestyles=['-'])
for i, score in enumerate(scores.values()):
    ax.text(i, score[0] + 0.002, '{:.6f}'.format(score[0]), horizontalalignment='left', size='large', color='black', weight='semibold')

plt.ylabel('Score (RMSE)', size=20, labelpad=12.5)
plt.xlabel('Model', size=20, labelpad=12.5)
plt.tick_params(axis='x', labelsize=13.5)
plt.tick_params(axis='y', labelsize=12.5)

plt.title('Scores of Models', size=20)

plt.show()

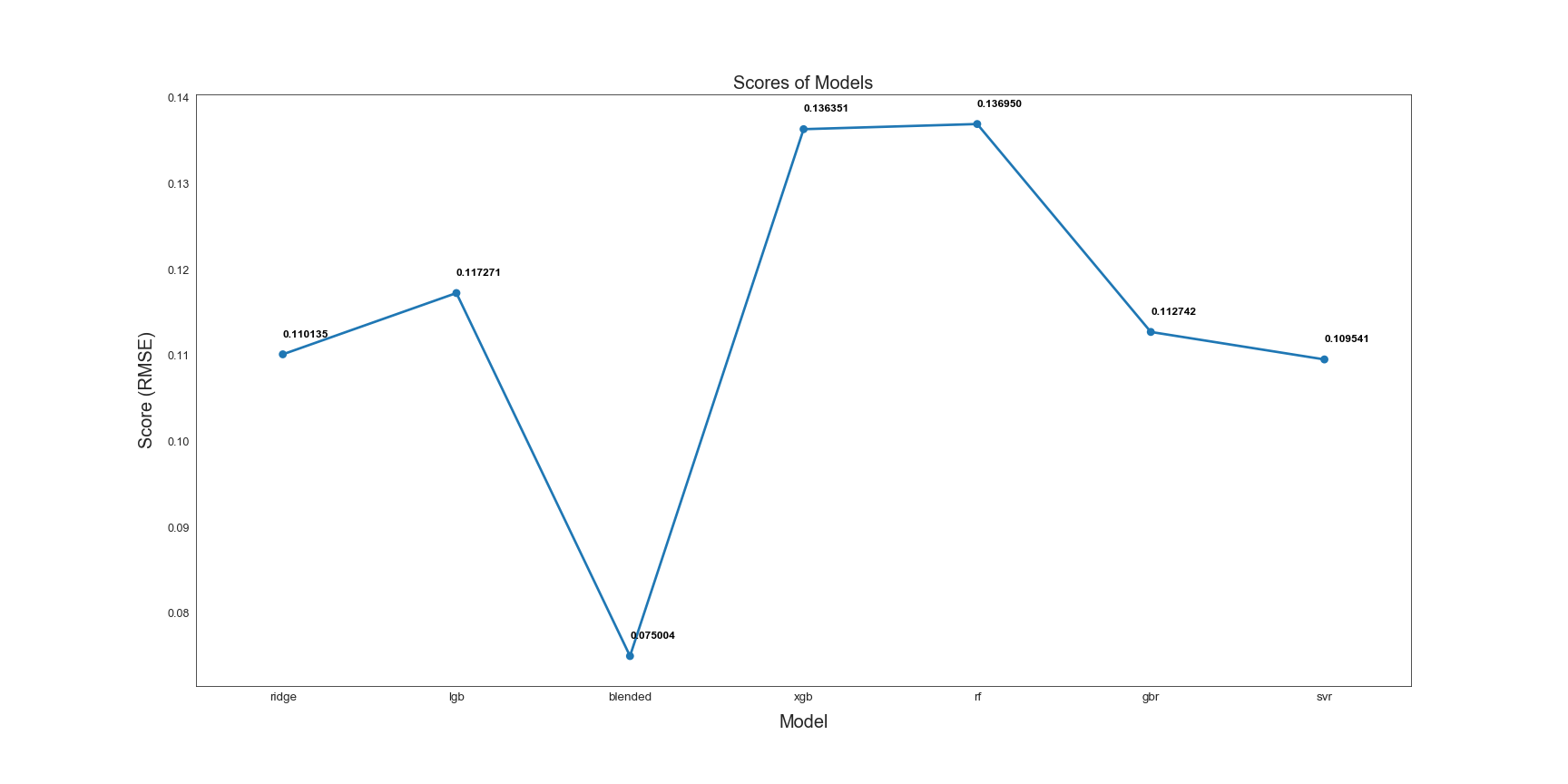
通过图中的展示可以看出，混合模型的结果明显优于其他模型，RMSE成绩为0.075。它也是最终预测中使用的模型。

到这里，愉快到模型训练结束了，通过我们的系列也可以看到，前期的特征工程花了3个系列才讲完，而模型训练一个系列就大功告成了，所以，不论是研究还是工业应用，特征工程才是重头戏啊，数据决定模型的上限。

有了得分不错的模型，我们就可以开始模型的部署和预测的执行了，这也是我们期待已久的重头戏。

首先，将待预测的测试集读取到 pandas 中：

submission = pd.read_csv("../input/house-prices-advanced-regression-techniques/sample_submission.csv")
submission.shape

其次，选择得分最好的混合模型进行预测，

submission.iloc[:,1] = np.floor(np.expm1(blended_predictions(X_test)))

在获得预测值后，对预测结果中的异常值进行修正：

q1 = submission['SalePrice'].quantile(0.0045)
q2 = submission['SalePrice'].quantile(0.99)
submission['SalePrice'] = submission['SalePrice'].apply(lambda x: x if x > q1 else x*0.77)
submission['SalePrice'] = submission['SalePrice'].apply(lambda x: x if x < q2 else x*1.1)
submission.to_csv("submission_regression1.csv", index=False)

最后，对预测结果保存，并进行评分判定。这里的 1.001619 也许让人有些疑惑，与上面权重的设定类似，这个值受到人主观的因素影响很大，可以看成是一个经验值，just worth to shot!

submission['SalePrice'] *= 1.001619
submission.to_csv("submission_regression2.csv", index=False)

至此，这个实战过程全部结束，通过这个过程可以看出，想要满意的模型，也需要台上5分钟，台下十年功的精神！