Kaggle房价预测实践系列1: 特征工程 EDA

在特征工程阶段，探索数据分析EDA是必不可少的部分。通过这一阶段对数据的观察分析，可以对数据的分布做一个宏观的了解，为后面数据的修正和调整确定一个基本的方向。

首先是对预测属性的数据观察

sns.set_style("white")
sns.set_color_codes(palette='deep')
f, ax = plt.subplots(figsize=(8, 7))
#Check the new distribution 
sns.distplot(train['SalePrice'], color="b");
(mu, sigma) = norm.fit(train['SalePrice'])
print( '\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
            loc='best')
ax.xaxis.grid(False)
ax.set(ylabel="Frequency")
ax.set(xlabel="SalePrice")
ax.set(title="SalePrice distribution")
sns.despine(trim=True, left=True)
plt.savefig("/Users/slyrx/slyrxStudio/github_good_projects/Tech_Blog/assets/images/sale_price_distribut.png")
plt.show()

png

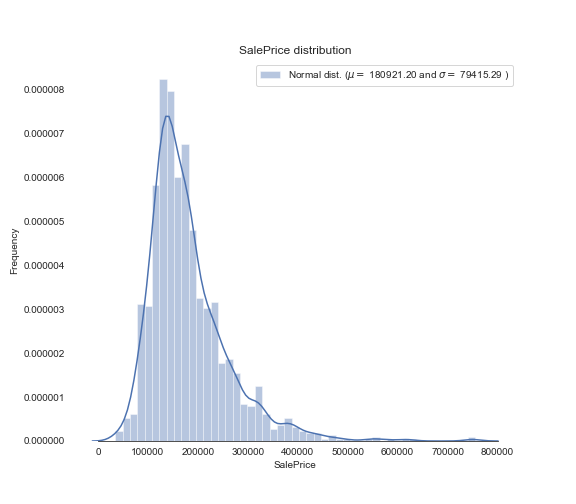
将此时的正态分布的斜度和峭度输出

print("Skewness: %f" % train['SalePrice'].skew())
print("Kurtosis: %f" % train['SalePrice'].kurt())

Skewness: 1.882876
Kurtosis: 6.536282

通常来说，我们期望数据分布能更加的趋于标准的正态分布，也就是说斜度和峭度能够更加的趋于：

Skewness: 0
Kurtosis: 3

那么，我们后续的努力就将朝着这个方向进行。从技术处理的角度来讲，对正态分布偏斜的修正使用对数函数log(1+x)进行修正。

train["SalePrice"] = np.log1p(train["SalePrice"])

我们再来看修正后的预测属性分布：

sns.set_style("white")
sns.set_color_codes(palette='deep')
f, ax = plt.subplots(figsize=(8, 7))

sns.distplot(train['SalePrice'], color="b");

(mu, sigma) = norm.fit(train['SalePrice'])
print( '\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
            loc='best')
ax.xaxis.grid(False)
ax.set(ylabel="Frequency")
ax.set(xlabel="SalePrice")
ax.set(title="SalePrice distribution")
sns.despine(trim=True, left=True)
plt.savefig("/Users/slyrx/slyrxStudio/github_good_projects/Tech_Blog/assets/images/sale_price_distribut_fixed.png")
plt.show()

png

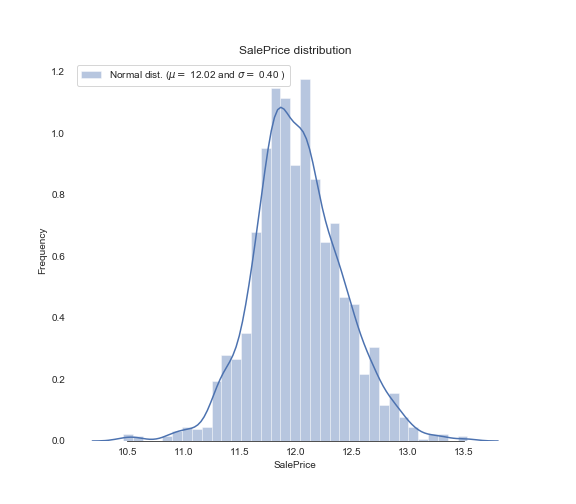
从模型的角度来讲，将数据修正为标准的正态分布是为了适应大多数的机器学习模型。现阶段，绝大多数的模型对于非正态分布的数据处理的并不好。

处理完预测属性，下面来处理特征数据。对于特征数据的分析，首先要将字符型特征和数值型特征进行区分，对于字符型特征需要将其先转换为数值型特征再进行分析，对于数值型的特征，已经有一系列成型的分析方法，具体流程包括：

	特征属性EDA过程
1.	散点图展示特征的分布情况
2.	混淆矩阵展示特征之间的相关性分布
3.	箱图展示预测属性与特征数据相关情况
4.	歪斜特征标准正态分布修正
5.	箱图展示特征正态分布情况

# Finding numeric features
numeric_dtypes = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
numeric = []
for i in train.columns:
    if train[i].dtype in numeric_dtypes:
        if i in ['TotalSF', 'Total_Bathrooms','Total_porch_sf','haspool','hasgarage','hasbsmt','hasfireplace']:
            pass
        else:
            numeric.append(i)  

fig, axs = plt.subplots(ncols=2, nrows=0, figsize=(12, 120))
plt.subplots_adjust(right=2)
plt.subplots_adjust(top=2)
sns.color_palette("husl", 8)
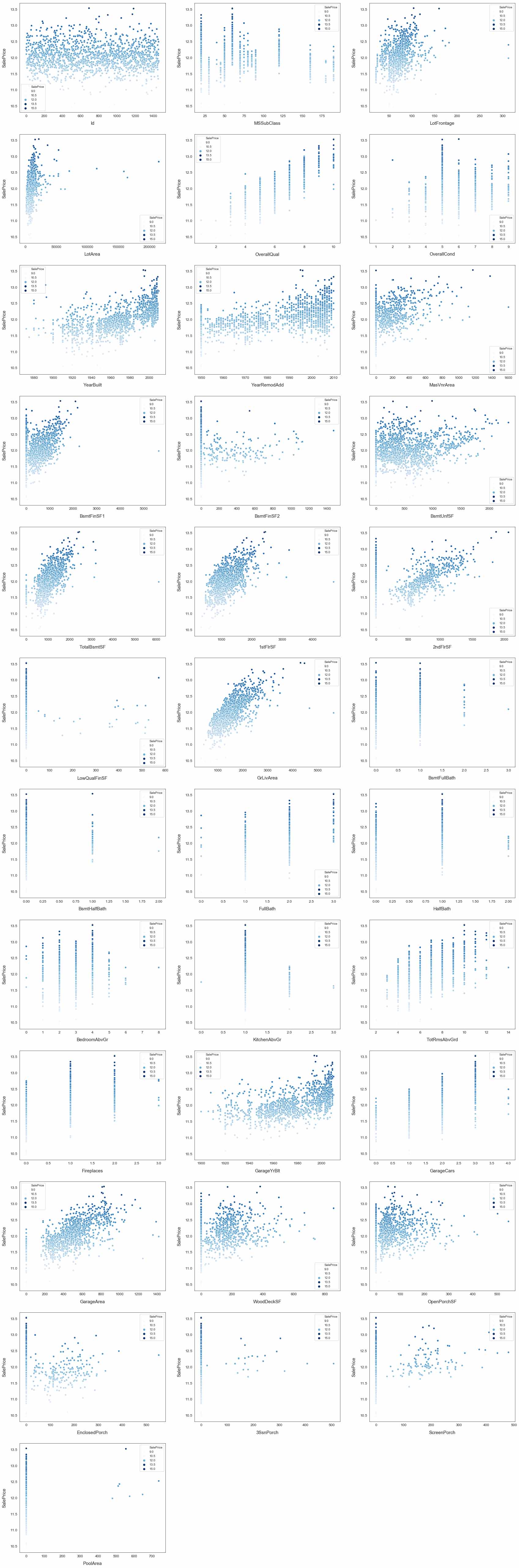
for i, feature in enumerate(list(train[numeric]), 1):
    if(feature=='MiscVal'):
        break
    plt.subplot(len(list(numeric)), 3, i)
    # 以散点图对内容进行展示
    sns.scatterplot(x=feature, y='SalePrice', hue='SalePrice', palette='Blues', data=train)
        
    plt.xlabel('{}'.format(feature), size=15,labelpad=12.5)
    plt.ylabel('SalePrice', size=15, labelpad=12.5)
    
    for j in range(2):
        plt.tick_params(axis='x', labelsize=12)
        plt.tick_params(axis='y', labelsize=12)
    
    plt.legend(loc='best', prop={'size': 10})

plt.savefig("/Users/slyrx/slyrxStudio/github_good_projects/Tech_Blog/assets/images/scatter_features_distribut.png")
plt.show()

png

通过图中观察可知，各个特征相对于预测属性，都存在一些离群点。特征数据的聚合度较好。那么，再来看一看这些特征之间的相关性如何

corr = train.corr()
plt.subplots(figsize=(15,12))
sns.heatmap(corr, vmax=0.9, cmap="Blues", square=True)

png

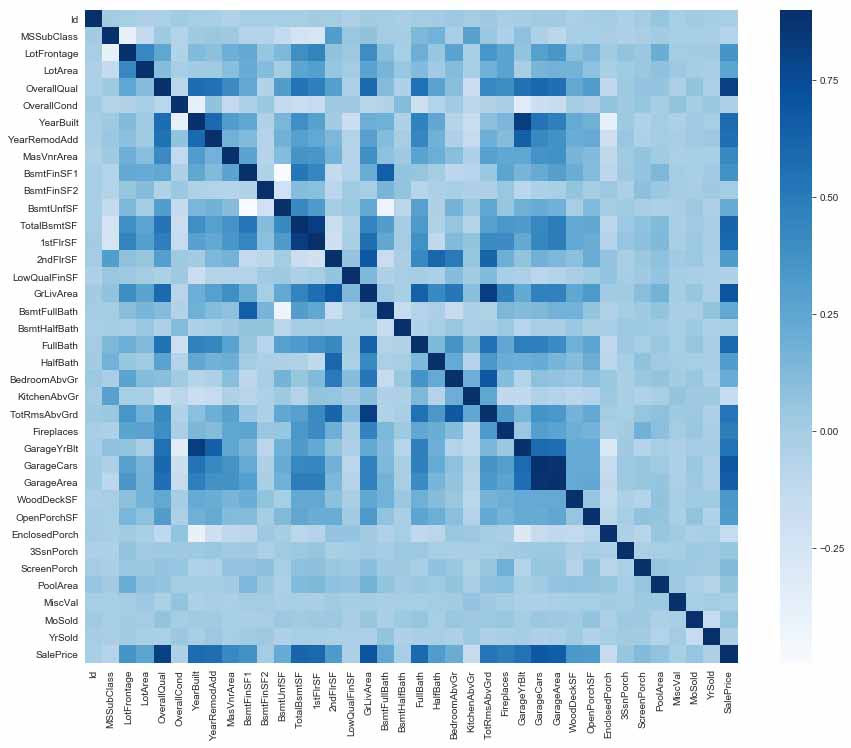
可以看到，图中颜色越深的地方，说明两者之间的特征相关性越强。而这里的预测属性与特征中的很多成员相关性都很强，因此，在模型的实际训练阶段，我们可以考虑将相关性强的特征移除，看看这种情况下的结果是否会更加的客观。

在具体分析，两个属性之间的相关性时，我们使用箱图来呈现。箱图是一种用作显示一组数据分散情况资料的统计图。主要用于反映原始数据分布的特征，还可以进行多组数据分布特征的比较。

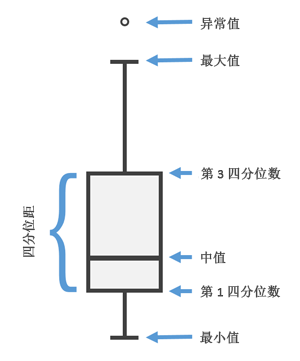以本例中，预测属性与 OverallQual 属性间的箱图为例，不同 OverallQual 属性对应的类别值呈现除了迥异的差别。1和2两种类别，可以较好的涵盖它们的数值特点，但是其他的几种类别则不同程度的涵盖着一些利群点。此阶段，我们需要记下这里的异常值情况，以期在后续的环节进行处理。

data = pd.concat([train['SalePrice'], train['OverallQual']], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x=train['OverallQual'], y="SalePrice", data=data)
fig.axis(ymin=10, ymax=15);
plt.savefig("/Users/slyrx/slyrxStudio/github_good_projects/Tech_Blog/assets/images/one_feature_box_map.png")

png

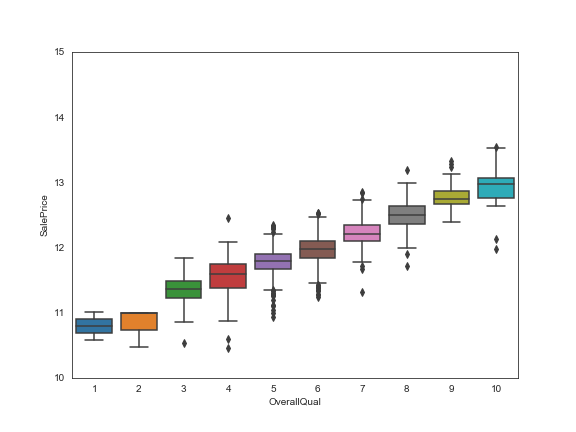
同样的，预测属性与其他特征之间的箱图，也可以逐个画出来，以供我们分析展示。

到这里，我们需要做的关于EDA的工作基本完结。下节将开始讲述特征工程的处理过程。